What’s greater than infinity?
My buddy James posted the status below to Facebook the other day, and I thought it was a great example of weird behavior that actually makes perfect sense…
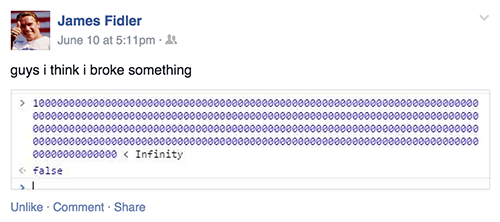
You see, Javascript uses 64-bit double-precision floating point numbers (aka doubles). Basically floating point numbers are numbers represented in scientific notation inside the computer, except that in scientific notation one typically uses base-10 whereas in floating point base-2 is used. This means that every floating point number is represented as 64 bits divvied up such that the first bit is the sign, the next bit is the exponent’s sign, the next 10 bits are for the exponent’s value, and the last 52 bits are for that mantissa (aka the significand).
The first bit is rather simple, 0 for positive, 1 for negative.
The next part is the exponent. It’s pretty simple as well, but there is one quirk. The IEEE standard was designed to allow the bits of a floating point number to be easily treated as an integer of the same size in order to allow for fast sorting and comparison; given that requirement the standard twos-complement representation couldn’t be used. Instead, the exponent is represented in a biased notation, in this case 1023 for 64-bit numbers. This means that 1023 is added to the exponent such that 0 is represented 1023, the minimum value of -1022 is represented as 1, and the maximum value of 1023 is represented as 2046 (0 and 2047 are reserved). This however is merely interesting and not really relevant to the question at hand. The point is the largest value the exponent can hold is \(2^{10} – 1\) or 1023.
The last component is the mantissa, but it’s really just the fractional part of the mantissa. Floating point numbers are stored in normalized form, meaning that the mantissa is defined to be \(1 \leq m < 2\). Given this, the first bit of the mantissa is always 1 and can therefore be assumed. As it doesn’t need to be stored only the fractional part of the mantissa is represented. This means that the maximum value of the mantissa gets very close to 2, but doesn’t quite reach it, in fact it’s: \(2-2^{-52}\).
Putting this all together leads us to the max integer value of:
\[2^{1023}*(2-2^{-52})=2^{1024}-2^{971} \approx 2^{1024} \approx 1.8*10^{308}\]Therefore, anything greater than that number is defined as being equal to infinity, which leads to the behavior encountered above.
But how do we represent infinity? And how do we represent 0 (if you were paying attention, the smallest mantissa you can have is 1)? Well, remember the two reserved exponent values, 0 and 2047, the were mentioned above? Infinity is defined to be a floating point number with an exponent of 2047 and a fractional field of 0. Similarly, an exponent of 0 and a fractional field of 0 is defined to be 0 (even though technically it’s not).
Loose the precision!Note: the above is for real numbers, the maximum safe integer value is \(2^{53} – 1\) (remember the way the bits were divvied up above), as once you start having to represent numbers in scientific notation you run the risk of losing (not loosing) precision.
Also note: I’m not a mathematician, I’m an engineer, I know enough about this stuff to keep myself from getting into trouble, but I’m probably terrible at explaining it. If you’re genuinely curious and want to know more Steve Hollasch has a great article on the subject.
